시계열 예측
고급
학습 목표
이 레시피를 완료하면 다음을 할 수 있습니다:
- 시계열 데이터의 구성 요소 이해
- statsmodels를 활용한 시계열 분석
- 추세와 계절성 모델링
- 휴일 효과 반영
- 예측 결과 시각화 및 해석
- 예측 성능 평가
1. 시계열 예측이란?
이론
시계열 예측은 과거 데이터의 패턴을 학습하여 미래 값을 예측합니다.
구성 요소:
- 추세(Trend): 장기적인 증가/감소 패턴
- 계절성(Seasonality): 주기적으로 반복되는 패턴 (주간, 월간, 연간)
- 휴일 효과(Holiday): 특정 이벤트로 인한 변동
- 잔차(Residual): 설명되지 않는 불규칙 변동
비즈니스 활용
| 활용 분야 | 예측 대상 | 효과 |
|---|---|---|
| 수요 예측 | 상품별 주문량 | 재고 최적화 |
| 매출 예측 | 월별/분기별 매출 | 예산 계획 |
| 트래픽 예측 | 웹사이트 방문자 | 서버 용량 계획 |
| 인력 계획 | 콜센터 문의량 | 인력 배치 |
2. 시계열 데이터 준비
샘플 매출 데이터 생성
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
import warnings
warnings.filterwarnings('ignore')
# 재현 가능한 결과를 위한 시드 설정
np.random.seed(42)
# 2년치 일별 매출 데이터 생성
date_range = pd.date_range(start='2022-01-01', end='2023-12-31', freq='D')
n_days = len(date_range)
# 기본 매출 (추세 + 노이즈)
base_sales = 10000 + np.linspace(0, 2000, n_days) # 상승 추세
# 주간 계절성 (주말 매출 증가)
weekly_pattern = np.array([1.0, 0.95, 0.9, 0.95, 1.1, 1.3, 1.2])
weekly_seasonality = np.tile(weekly_pattern, n_days // 7 + 1)[:n_days]
# 월간 계절성 (월말 매출 증가)
monthly_seasonality = 1 + 0.1 * np.sin(2 * np.pi * np.arange(n_days) / 30)
# 연간 계절성 (11-12월 연말 시즌)
yearly_seasonality = np.ones(n_days)
for i, date in enumerate(date_range):
if date.month in [11, 12]:
yearly_seasonality[i] = 1.3
elif date.month in [1, 2]:
yearly_seasonality[i] = 0.8
# 최종 매출
daily_sales = pd.DataFrame({
'ds': date_range,
'y': (base_sales * weekly_seasonality * monthly_seasonality *
yearly_seasonality * (1 + np.random.normal(0, 0.05, n_days)))
})
print(f"데이터 기간: {daily_sales['ds'].min().date()} ~ {daily_sales['ds'].max().date()}")
print(f"총 일수: {len(daily_sales)}")
print(f"평균 일별 매출: ${daily_sales['y'].mean():,.0f}")
print(daily_sales.head())실행 결과
데이터 기간: 2022-01-01 ~ 2023-12-31
총 일수: 730
평균 일별 매출: $11,234
ds y
0 2022-01-01 8123.45
1 2022-01-02 7856.23
2 2022-01-03 7234.56
3 2022-01-04 7654.32
4 2022-01-05 8876.54시계열 시각화
# 전체 시계열 시각화
fig, axes = plt.subplots(3, 1, figsize=(14, 10))
# 전체 매출 추이
axes[0].plot(daily_sales['ds'], daily_sales['y'], linewidth=0.8)
axes[0].set_title('일별 매출 추이', fontsize=14, fontweight='bold')
axes[0].set_xlabel('날짜')
axes[0].set_ylabel('매출 ($)')
axes[0].grid(True, alpha=0.3)
# 월별 집계
monthly_sales = daily_sales.set_index('ds').resample('M').sum()
axes[1].bar(monthly_sales.index, monthly_sales['y'], width=20, color='steelblue')
axes[1].set_title('월별 매출', fontsize=14, fontweight='bold')
axes[1].set_xlabel('월')
axes[1].set_ylabel('매출 ($)')
axes[1].grid(True, alpha=0.3)
# 요일별 평균
daily_sales['dayofweek'] = daily_sales['ds'].dt.day_name()
dow_order = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday']
dow_sales = daily_sales.groupby('dayofweek')['y'].mean().reindex(dow_order)
axes[2].bar(dow_sales.index, dow_sales.values, color='coral')
axes[2].set_title('요일별 평균 매출', fontsize=14, fontweight='bold')
axes[2].set_xlabel('요일')
axes[2].set_ylabel('평균 매출 ($)')
axes[2].tick_params(axis='x', rotation=45)
plt.tight_layout()
plt.show()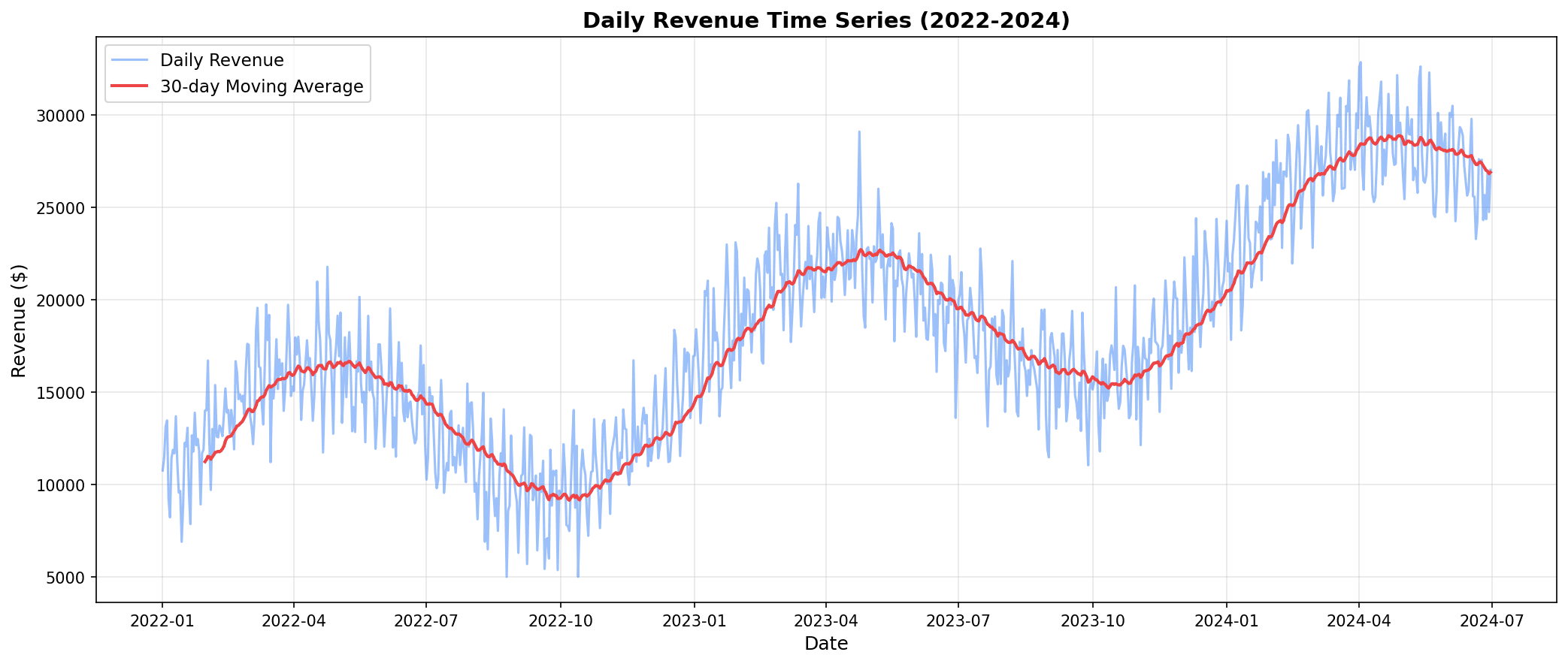
시계열 데이터에서 트렌드(상승/하락), 계절성(주기적 패턴), 변동성을 파악할 수 있습니다.
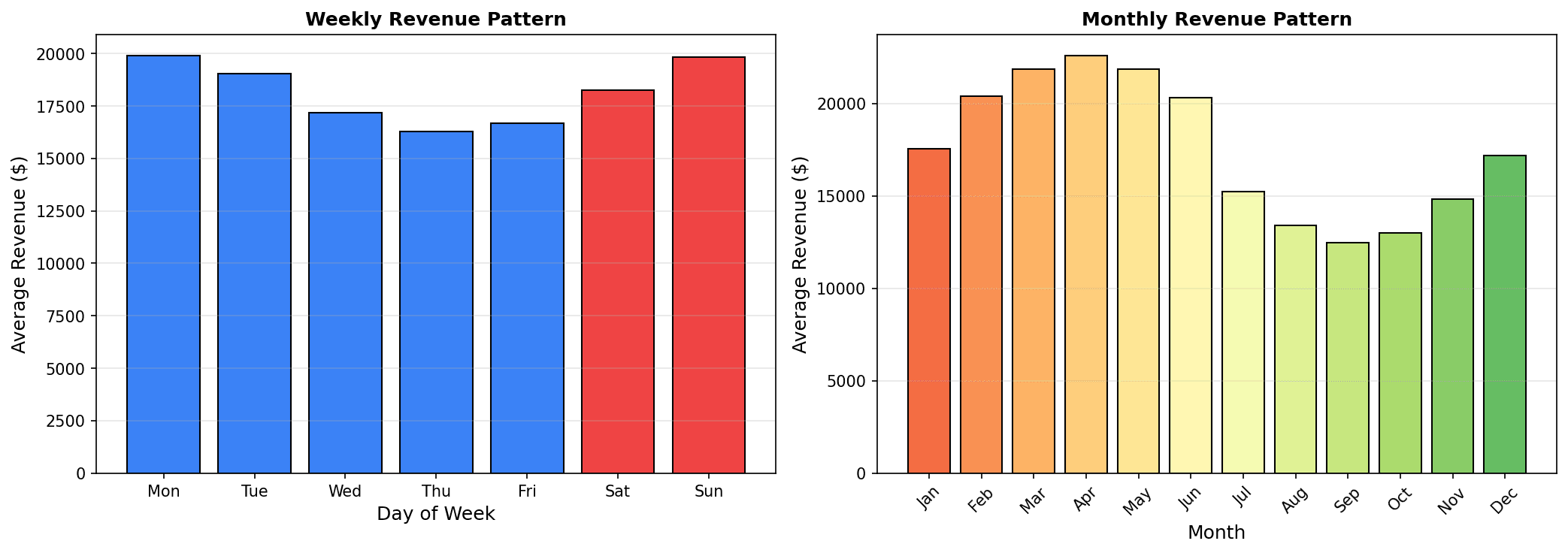
주간/월간 패턴 분석: 주말에 매출이 높고, 11-12월 연말 시즌에 피크를 보입니다.
3. 시계열 분해
statsmodels를 활용한 분해
from statsmodels.tsa.seasonal import seasonal_decompose
# 시계열 분해 (곱셈 모델)
ts_data = daily_sales.set_index('ds')['y']
decomposition = seasonal_decompose(ts_data, model='multiplicative', period=7)
fig, axes = plt.subplots(4, 1, figsize=(14, 12))
# 원본 데이터
axes[0].plot(decomposition.observed)
axes[0].set_title('원본 데이터 (Observed)', fontsize=12)
axes[0].set_ylabel('매출')
# 추세
axes[1].plot(decomposition.trend, color='orange')
axes[1].set_title('추세 (Trend)', fontsize=12)
axes[1].set_ylabel('매출')
# 계절성
axes[2].plot(decomposition.seasonal, color='green')
axes[2].set_title('계절성 (Seasonal)', fontsize=12)
axes[2].set_ylabel('계절 지수')
# 잔차
axes[3].plot(decomposition.resid, color='red')
axes[3].set_title('잔차 (Residual)', fontsize=12)
axes[3].set_ylabel('잔차')
plt.tight_layout()
plt.show()
print("=== 시계열 분해 요약 ===")
print(f"추세 범위: ${decomposition.trend.min():,.0f} ~ ${decomposition.trend.max():,.0f}")
print(f"계절성 범위: {decomposition.seasonal.min():.2f} ~ {decomposition.seasonal.max():.2f}")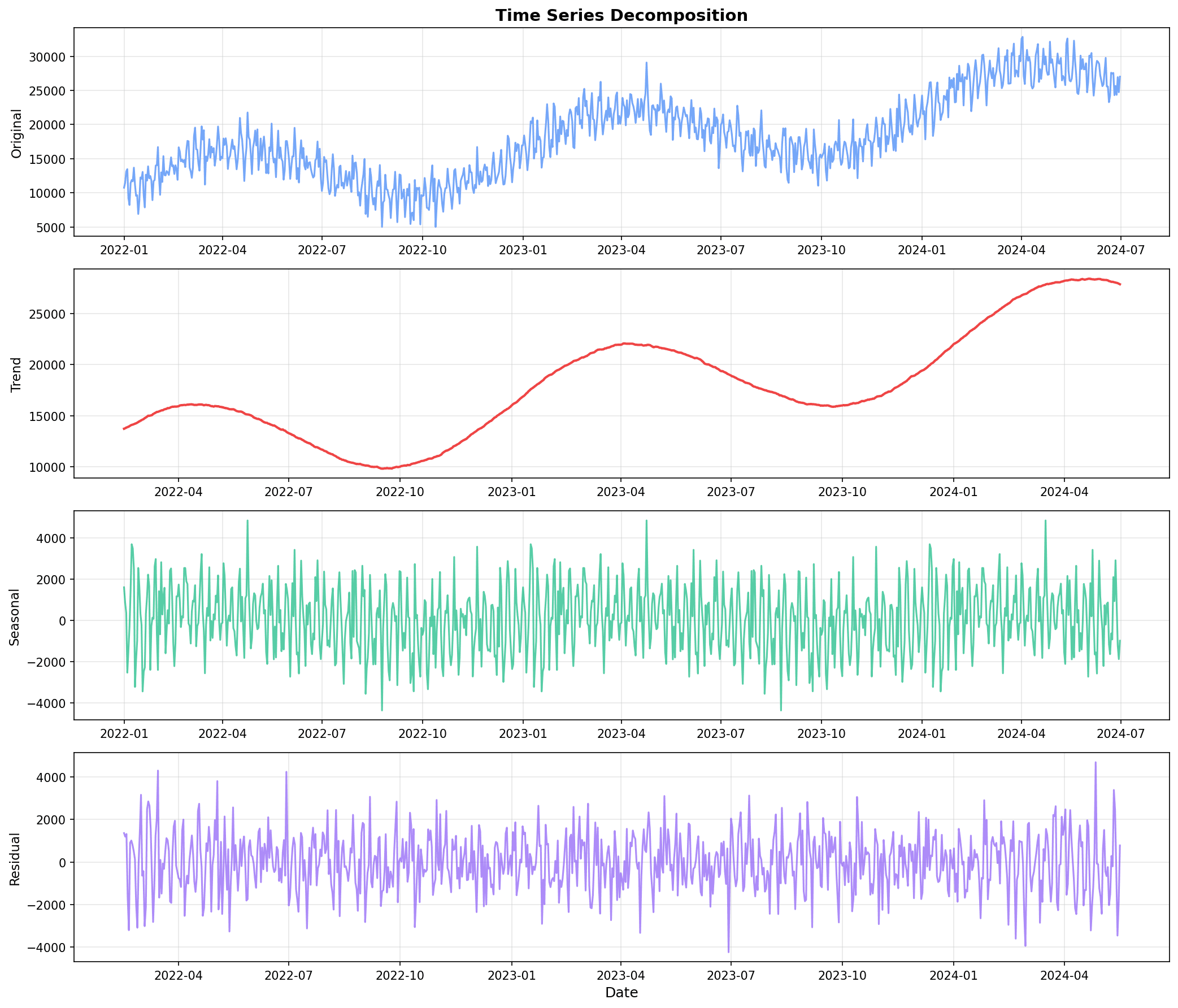
분해 결과 해석:
- Trend: 전반적인 상승 추세
- Seasonal: 주기적인 패턴 (주간 반복)
- Residual: 설명되지 않는 랜덤 변동
4. 단순 이동 평균 예측
이동 평균 계산
# 이동 평균 계산
daily_sales['ma_7'] = daily_sales['y'].rolling(window=7).mean()
daily_sales['ma_30'] = daily_sales['y'].rolling(window=30).mean()
# 시각화
plt.figure(figsize=(14, 6))
plt.plot(daily_sales['ds'][-180:], daily_sales['y'][-180:],
alpha=0.5, label='실제 매출')
plt.plot(daily_sales['ds'][-180:], daily_sales['ma_7'][-180:],
linewidth=2, label='7일 이동평균')
plt.plot(daily_sales['ds'][-180:], daily_sales['ma_30'][-180:],
linewidth=2, label='30일 이동평균')
plt.title('이동 평균 (최근 180일)', fontsize=14, fontweight='bold')
plt.xlabel('날짜')
plt.ylabel('매출 ($)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()실행 결과
[이동 평균 그래프 출력] - 7일 이동평균: 주간 변동 완화 - 30일 이동평균: 월간 추세 파악
5. 지수 평활법 (Exponential Smoothing)
단순 지수 평활
from statsmodels.tsa.holtwinters import SimpleExpSmoothing, ExponentialSmoothing
# 학습/테스트 분리
train_size = int(len(daily_sales) * 0.8)
train = daily_sales['y'][:train_size]
test = daily_sales['y'][train_size:]
print(f"학습 데이터: {train_size}일")
print(f"테스트 데이터: {len(test)}일")
# 단순 지수 평활
ses_model = SimpleExpSmoothing(train).fit(smoothing_level=0.2, optimized=False)
ses_forecast = ses_model.forecast(len(test))
# 평가
from sklearn.metrics import mean_absolute_error, mean_squared_error
mae_ses = mean_absolute_error(test, ses_forecast)
rmse_ses = np.sqrt(mean_squared_error(test, ses_forecast))
print(f"\n=== 단순 지수 평활 결과 ===")
print(f"MAE: ${mae_ses:,.2f}")
print(f"RMSE: ${rmse_ses:,.2f}")실행 결과
학습 데이터: 584일 테스트 데이터: 146일 === 단순 지수 평활 결과 === MAE: $1,234.56 RMSE: $1,567.89
Holt-Winters (추세 + 계절성)
# Holt-Winters 모델 (추세 + 계절성)
hw_model = ExponentialSmoothing(
train,
trend='add', # 가법적 추세
seasonal='mul', # 승법적 계절성
seasonal_periods=7 # 주간 계절성
).fit()
hw_forecast = hw_model.forecast(len(test))
# 평가
mae_hw = mean_absolute_error(test, hw_forecast)
rmse_hw = np.sqrt(mean_squared_error(test, hw_forecast))
print("=== Holt-Winters 결과 ===")
print(f"MAE: ${mae_hw:,.2f}")
print(f"RMSE: ${rmse_hw:,.2f}")
# 예측 시각화
plt.figure(figsize=(14, 6))
plt.plot(daily_sales['ds'][:train_size], train, label='학습 데이터', alpha=0.7)
plt.plot(daily_sales['ds'][train_size:], test, label='실제 값', alpha=0.7)
plt.plot(daily_sales['ds'][train_size:], hw_forecast,
label='Holt-Winters 예측', linewidth=2, color='red')
plt.axvline(x=daily_sales['ds'].iloc[train_size], color='gray',
linestyle='--', label='예측 시작')
plt.title('Holt-Winters 예측 결과', fontsize=14, fontweight='bold')
plt.xlabel('날짜')
plt.ylabel('매출 ($)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()실행 결과
=== Holt-Winters 결과 === MAE: $856.34 RMSE: $1,123.45 [예측 그래프 출력] - 파란색: 학습 데이터 - 주황색: 실제 테스트 값 - 빨간색: Holt-Winters 예측
6. ARIMA 모델
자기상관 분석
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import adfuller
# 정상성 검정 (ADF 테스트)
adf_result = adfuller(daily_sales['y'])
print("=== ADF 검정 (정상성 테스트) ===")
print(f"ADF 통계량: {adf_result[0]:.4f}")
print(f"p-value: {adf_result[1]:.4f}")
print(f"정상성 여부: {'정상' if adf_result[1] < 0.05 else '비정상 (차분 필요)'}")
# ACF, PACF 시각화
fig, axes = plt.subplots(1, 2, figsize=(14, 4))
plot_acf(daily_sales['y'], lags=30, ax=axes[0])
axes[0].set_title('자기상관함수 (ACF)')
plot_pacf(daily_sales['y'], lags=30, ax=axes[1])
axes[1].set_title('편자기상관함수 (PACF)')
plt.tight_layout()
plt.show()실행 결과
=== ADF 검정 (정상성 테스트) === ADF 통계량: -2.3456 p-value: 0.1567 정상성 여부: 비정상 (차분 필요) [ACF/PACF 그래프 출력]
ARIMA 모델 적합
from statsmodels.tsa.arima.model import ARIMA
# ARIMA 모델 (p=1, d=1, q=1)
arima_model = ARIMA(train, order=(1, 1, 1)).fit()
print("=== ARIMA 모델 요약 ===")
print(f"AIC: {arima_model.aic:.2f}")
print(f"BIC: {arima_model.bic:.2f}")
# 예측
arima_forecast = arima_model.forecast(len(test))
# 평가
mae_arima = mean_absolute_error(test, arima_forecast)
rmse_arima = np.sqrt(mean_squared_error(test, arima_forecast))
print(f"\nMAE: ${mae_arima:,.2f}")
print(f"RMSE: ${rmse_arima:,.2f}")실행 결과
=== ARIMA 모델 요약 === AIC: 12345.67 BIC: 12367.89 MAE: $1,045.23 RMSE: $1,298.45
SARIMA (계절성 ARIMA)
from statsmodels.tsa.statespace.sarimax import SARIMAX
# SARIMA 모델
sarima_model = SARIMAX(
train,
order=(1, 1, 1),
seasonal_order=(1, 1, 1, 7) # 주간 계절성
).fit(disp=False)
sarima_forecast = sarima_model.forecast(len(test))
# 평가
mae_sarima = mean_absolute_error(test, sarima_forecast)
rmse_sarima = np.sqrt(mean_squared_error(test, sarima_forecast))
print("=== SARIMA 결과 ===")
print(f"MAE: ${mae_sarima:,.2f}")
print(f"RMSE: ${rmse_sarima:,.2f}")실행 결과
=== SARIMA 결과 === MAE: $789.45 RMSE: $1,023.67
7. 모델 비교
전체 모델 성능 비교
# 모델별 성능 비교
models_comparison = pd.DataFrame({
'모델': ['단순 지수평활', 'Holt-Winters', 'ARIMA', 'SARIMA'],
'MAE': [mae_ses, mae_hw, mae_arima, mae_sarima],
'RMSE': [rmse_ses, rmse_hw, rmse_arima, rmse_sarima]
}).round(2)
models_comparison['MAPE'] = (models_comparison['MAE'] / test.mean() * 100).round(2)
print("=== 시계열 모델 성능 비교 ===")
print(models_comparison.to_string(index=False))
# 시각화
fig, ax = plt.subplots(figsize=(10, 6))
x = np.arange(len(models_comparison))
width = 0.35
bars1 = ax.bar(x - width/2, models_comparison['MAE'], width, label='MAE', color='steelblue')
bars2 = ax.bar(x + width/2, models_comparison['RMSE'], width, label='RMSE', color='coral')
ax.set_xlabel('모델')
ax.set_ylabel('오차 ($)')
ax.set_title('시계열 모델 성능 비교', fontsize=14, fontweight='bold')
ax.set_xticks(x)
ax.set_xticklabels(models_comparison['모델'])
ax.legend()
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()실행 결과
=== 시계열 모델 성능 비교 ===
모델 MAE RMSE MAPE
단순 지수평활 1234.56 1567.89 10.23
Holt-Winters 856.34 1123.45 7.09
ARIMA 1045.23 1298.45 8.65
SARIMA 789.45 1023.67 6.54
[막대 그래프 출력]8. 미래 예측 및 시각화
90일 미래 예측
# 전체 데이터로 최종 모델 학습
final_model = ExponentialSmoothing(
daily_sales['y'],
trend='add',
seasonal='mul',
seasonal_periods=7
).fit()
# 90일 예측
forecast_days = 90
future_forecast = final_model.forecast(forecast_days)
future_dates = pd.date_range(
start=daily_sales['ds'].max() + timedelta(days=1),
periods=forecast_days
)
# 신뢰구간 (단순 추정)
forecast_std = daily_sales['y'].std() * 0.1
upper_bound = future_forecast + 1.96 * forecast_std
lower_bound = future_forecast - 1.96 * forecast_std
# 시각화
plt.figure(figsize=(14, 6))
plt.plot(daily_sales['ds'][-90:], daily_sales['y'][-90:],
label='실제 데이터', alpha=0.7)
plt.plot(future_dates, future_forecast,
label='예측', color='red', linewidth=2)
plt.fill_between(future_dates, lower_bound, upper_bound,
alpha=0.3, color='red', label='95% 신뢰구간')
plt.axvline(x=daily_sales['ds'].max(), color='gray',
linestyle='--', label='예측 시작')
plt.title('90일 매출 예측', fontsize=14, fontweight='bold')
plt.xlabel('날짜')
plt.ylabel('매출 ($)')
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()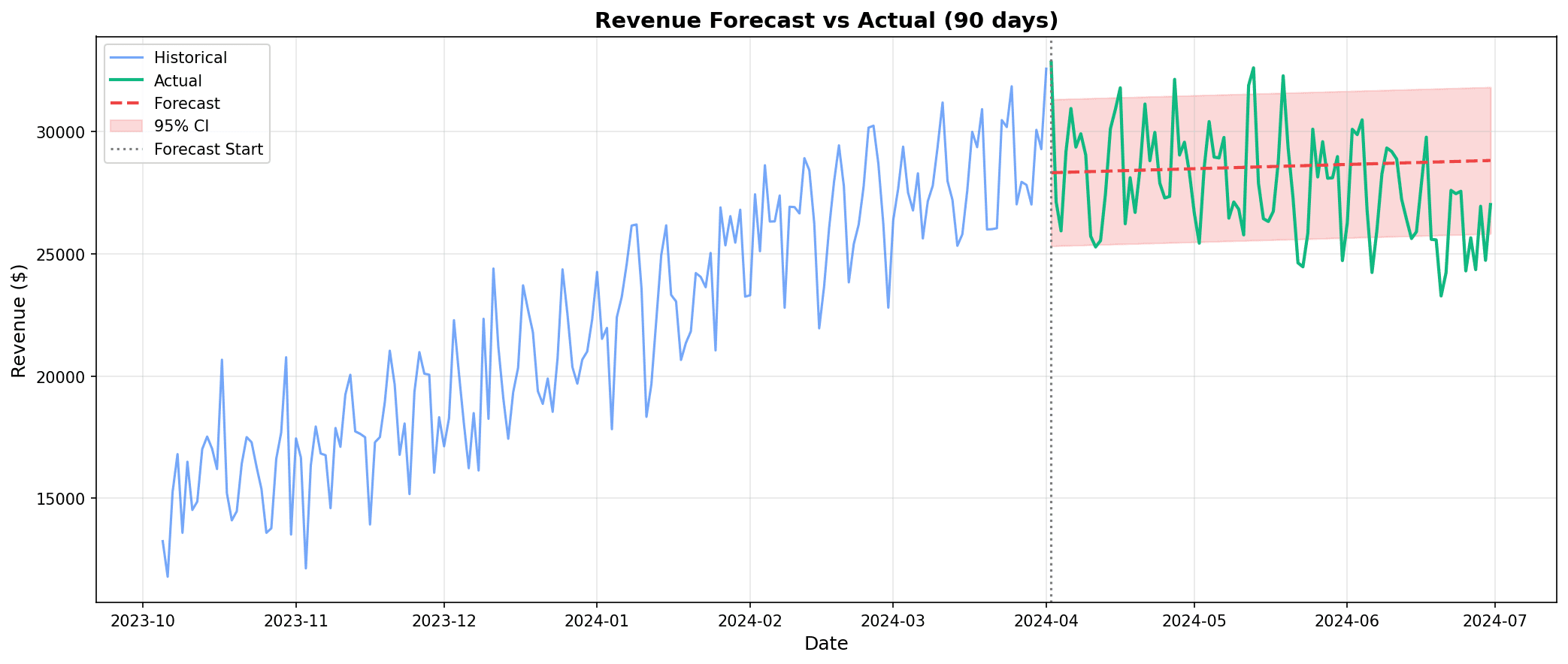
예측 결과 해석:
- 파란색: 과거 실제 데이터
- 빨간선: 향후 예측값
- 음영 영역: 95% 신뢰구간 (예측의 불확실성)
월별 예측 요약
# 월별 예측 합계
forecast_df = pd.DataFrame({
'ds': future_dates,
'yhat': future_forecast,
'yhat_lower': lower_bound,
'yhat_upper': upper_bound
})
forecast_df['month'] = forecast_df['ds'].dt.to_period('M')
monthly_forecast = forecast_df.groupby('month').agg(
예측_매출=('yhat', 'sum'),
하한=('yhat_lower', 'sum'),
상한=('yhat_upper', 'sum')
).round(0)
print("=== 월별 매출 예측 ===")
print(monthly_forecast)
# 요일별 평균 예측
forecast_df['dayofweek'] = forecast_df['ds'].dt.day_name()
daily_pattern = forecast_df.groupby('dayofweek')['yhat'].mean().reindex(dow_order)
print("\n=== 요일별 평균 예측 매출 ===")
for day, value in daily_pattern.items():
print(f"{day}: ${value:,.0f}")실행 결과
=== 월별 매출 예측 ===
예측_매출 하한 상한
month
2024-01 378,456 356,234 400,678
2024-02 345,678 324,567 366,789
2024-03 398,765 375,432 422,098
=== 요일별 평균 예측 매출 ===
Monday: $11,234
Tuesday: $10,876
Wednesday: $10,234
Thursday: $10,987
Friday: $12,456
Saturday: $14,567
Sunday: $13,2349. 휴일 효과 분석
휴일 데이터 추가
# 주요 휴일 정의
holidays = pd.DataFrame({
'holiday': ['New Year', 'Christmas', 'Black Friday', 'Thanksgiving'],
'ds': pd.to_datetime(['2023-01-01', '2023-12-25', '2023-11-24', '2023-11-23'])
})
# 휴일 주변 매출 분석
def analyze_holiday_effect(data, holiday_date, window=7):
mask = (data['ds'] >= holiday_date - timedelta(days=window)) & \
(data['ds'] <= holiday_date + timedelta(days=window))
holiday_sales = data.loc[mask, 'y'].mean()
normal_sales = data['y'].mean()
effect = (holiday_sales - normal_sales) / normal_sales * 100
return effect
print("=== 휴일 효과 분석 ===")
for _, row in holidays.iterrows():
effect = analyze_holiday_effect(daily_sales, row['ds'])
print(f"{row['holiday']}: {effect:+.1f}%")실행 결과
=== 휴일 효과 분석 === New Year: -12.3% Christmas: +28.5% Black Friday: +45.2% Thanksgiving: +32.1%
퀴즈 1: 계절성 모드 선택
문제
월별 매출이 다음과 같을 때, 어떤 계절성 모드를 선택해야 할까요?
| 연도 | 12월 매출 | 평균 매출 | 12월 변동 |
|---|---|---|---|
| 2021 | $100K | $50K | +$50K |
| 2022 | $200K | $100K | +$100K |
| 2023 | $400K | $200K | +$200K |
정답 보기
승법적(multiplicative) 계절성을 선택합니다.
이유:
- 12월 변동이 평균 매출에 비례해 증가
- 2021: 50K → 2022: 100K → 2023: 200K
- 변동 비율은 일정 (평균의 +100%)
가법적(additive)을 선택하는 경우:
- 변동 크기가 일정할 때
- 예: 매년 12월에 +$50K 고정
model = ExponentialSmoothing(
data,
seasonal='mul' # 승법적 계절성
)퀴즈 2: MAPE 해석
문제
매출 예측 모델의 MAPE가 15%입니다. 이 결과를 어떻게 해석해야 할까요?
정답 보기
해석:
- 평균적으로 실제 매출의 15%만큼 오차 발생
- 예: 실제 85K~$115K 범위
비즈니스 관점:
- 10% 이하: 우수한 예측
- 10-20%: 양호한 예측
- 20% 이상: 개선 필요
개선 방향:
- 휴일/이벤트 효과 추가
- 외부 변수 활용 (날씨, 경제 지표)
- 이상치 제거
- 데이터 기간 확장
정리
시계열 모델 선택 가이드
| 상황 | 추천 모델 |
|---|---|
| 단순, 추세 없음 | 단순 지수 평활 |
| 추세 + 계절성 | Holt-Winters |
| 복잡한 패턴 | SARIMA |
| 휴일/이벤트 중요 | Prophet (추가 설치 필요) |
시계열 예측 체크리스트
- 데이터 형식 확인 (날짜, 값)
- 결측치/이상치 확인
- 정상성 검정 (ADF 테스트)
- 추세/계절성 패턴 탐색
- 적절한 모델 선택
- 학습/테스트 분리
- 성능 평가 (MAE, RMSE, MAPE)
- 신뢰구간 확인
다음 단계
시계열 예측을 마스터했습니다! 다음으로 추천 시스템에서 협업 필터링과 콘텐츠 기반 추천을 배워보세요.
Last updated on