분포 시각화

초급중급

학습 목표

이 레시피를 완료하면 다음을 할 수 있습니다:

히스토그램으로 데이터 분포 파악
박스플롯으로 이상치 탐지
바이올린 플롯으로 분포 비교
KDE 플롯으로 밀도 추정

0. 사전 준비 (Setup)

데이터 실습을 위해 CSV 파일을 로드합니다.


import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
 
# Load Data
# Load Data
orders = pd.read_csv('src_orders.csv', parse_dates=['created_at'])
items = pd.read_csv('src_order_items.csv')
users = pd.read_csv('src_users.csv')
df = orders.merge(items, on='order_id').merge(users, on='user_id')

1. 히스토그램

이론

히스토그램은 연속형 데이터를 구간(bin)으로 나누어 빈도를 막대로 표현합니다. 데이터의 분포 형태(정규, 왜도, 이봉 등)를 파악하는 데 유용합니다.

기본 히스토그램


import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
 
# 기본 히스토그램
plt.figure(figsize=(12, 5))
 
plt.subplot(1, 2, 1)
plt.hist(df['sale_price'], bins=30, color='steelblue', edgecolor='white', alpha=0.7)
plt.title('Sale Price Distribution (Matplotlib)', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
plt.ylabel('Frequency')
 
plt.subplot(1, 2, 2)
sns.histplot(df['sale_price'], bins=30, kde=True, color='coral')
plt.title('Sale Price Distribution (Seaborn + KDE)', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
 
plt.tight_layout()
plt.show()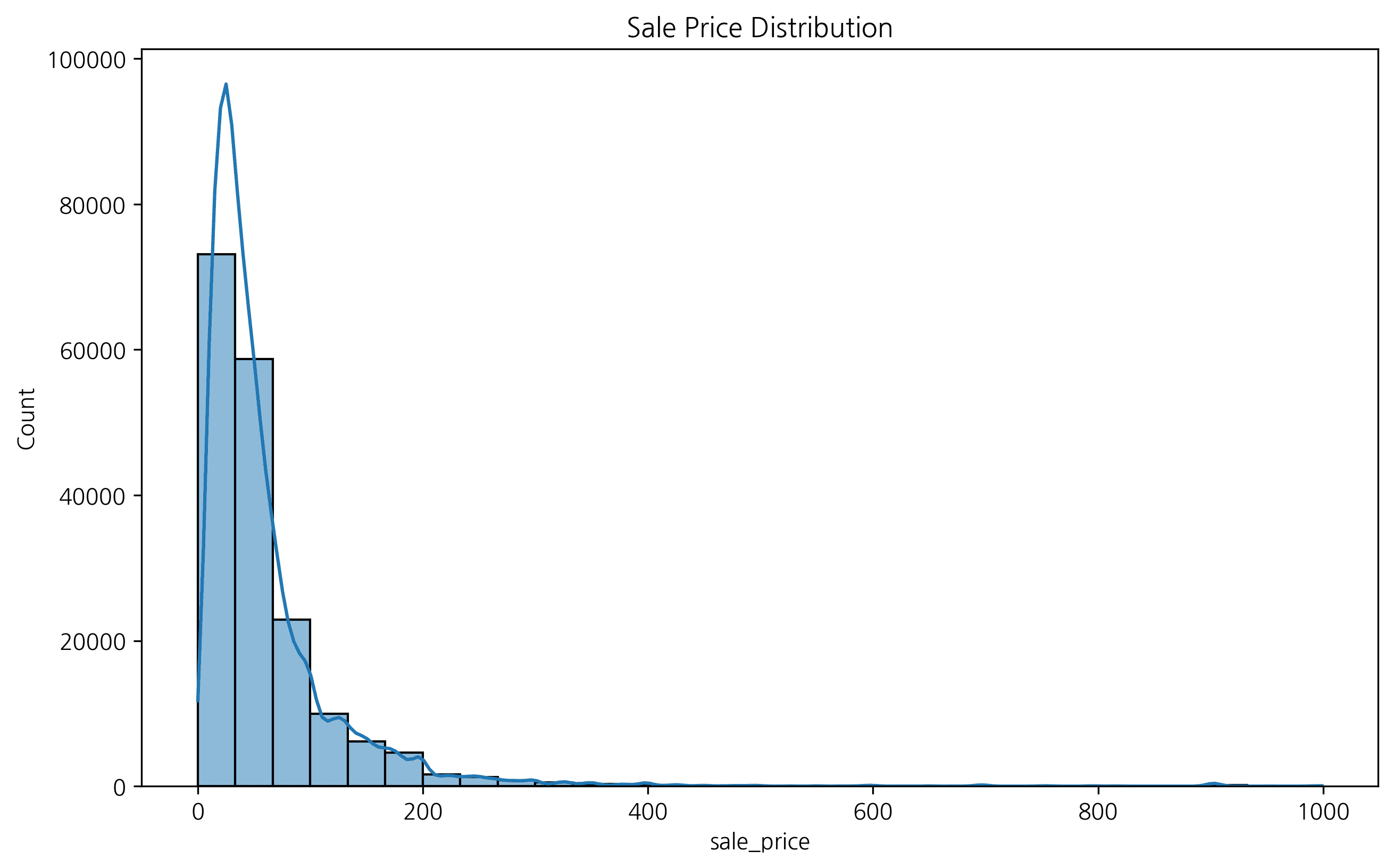

Histogram

2. 구간(Bin) 개수 설정

bins 파라미터로 히스토그램의 막대 개수를 조절할 수 있습니다. 구간 설정에 따라 데이터 해석이 달라질 수 있습니다.


fig, axes = plt.subplots(1, 3, figsize=(15, 5))
 
sns.histplot(df['sale_price'], bins=10, ax=axes[0], color='skyblue')
axes[0].set_title('Bins = 10')
 
sns.histplot(df['sale_price'], bins=30, ax=axes[1], color='orange')
axes[1].set_title('Bins = 30')
 
sns.histplot(df['sale_price'], bins=50, ax=axes[2], color='green')
axes[2].set_title('Bins = 50')
 
plt.tight_layout()
plt.show()

Histogram Bins Comparison

ℹ️

구간이 너무 적으면 데이터의 특징이 뭉개지고, 너무 많으면 노이즈가 심해질 수 있습니다. 적절한 bins 설정이 중요합니다.

3. 그룹별 히스토그램 (Grouped Histogram)

범주형 변수에 따라 데이터 분포가 어떻게 다른지 비교할 수 있습니다. 예를 들어, 성별에 따른 판매 가격 분포를 확인해 봅니다.


plt.figure(figsize=(10, 6))
sns.histplot(data=df, x='sale_price', hue='gender', kde=True, element='step')
plt.title('Sale Price Distribution by Gender')
plt.xlabel('Sale Price')
plt.ylabel('Count')
plt.legend(title='Gender')
plt.show()

Grouped Histogram

4. 박스 플롯 (Box Plot)

데이터의 분포와 이상치(Outlier)를 한눈에 파악하기 좋습니다.


plt.figure(figsize=(12, 6))
sns.boxplot(x='category', y='sale_price', data=df)
plt.xticks(rotation=45)
plt.title('Price Distribution by Category')
plt.show()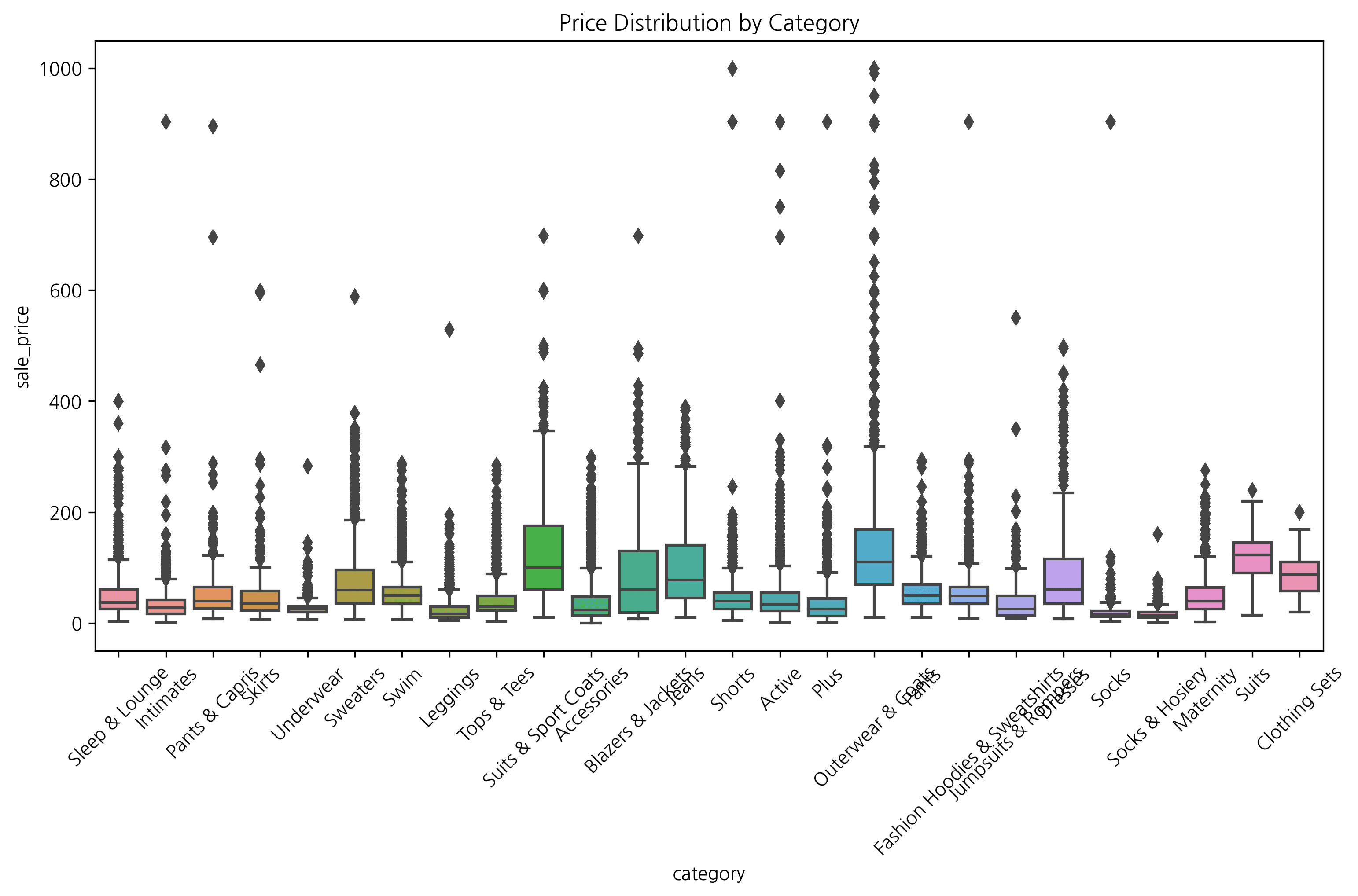

Box Plot

2. 박스플롯

이론

박스플롯은 데이터의 5가지 요약 통계량(최소, Q1, 중앙값, Q3, 최대)과 이상치를 시각화합니다.

박스플롯 구성:

박스: Q1 ~ Q3 (IQR)
중앙선: 중앙값 (median)
수염: Q1 - 1.5×IQR ~ Q3 + 1.5×IQR
점: 이상치 (outliers)

기본 박스플롯


plt.figure(figsize=(12, 5))
 
# Matplotlib
plt.subplot(1, 2, 1)
plt.boxplot(df['sale_price'].dropna())
plt.title('가격 분포 (Matplotlib)', fontsize=14, fontweight='bold')
plt.ylabel('판매가격 ($)')
 
# Seaborn (수평)
plt.subplot(1, 2, 2)
sns.boxplot(x=df['sale_price'], color='lightblue')
plt.title('가격 분포 (Seaborn)', fontsize=14, fontweight='bold')
plt.xlabel('판매가격 ($)')
 
plt.tight_layout()
plt.show()

실행 결과

[Graph Saved: generated_plot_1d8420747f_0.png]

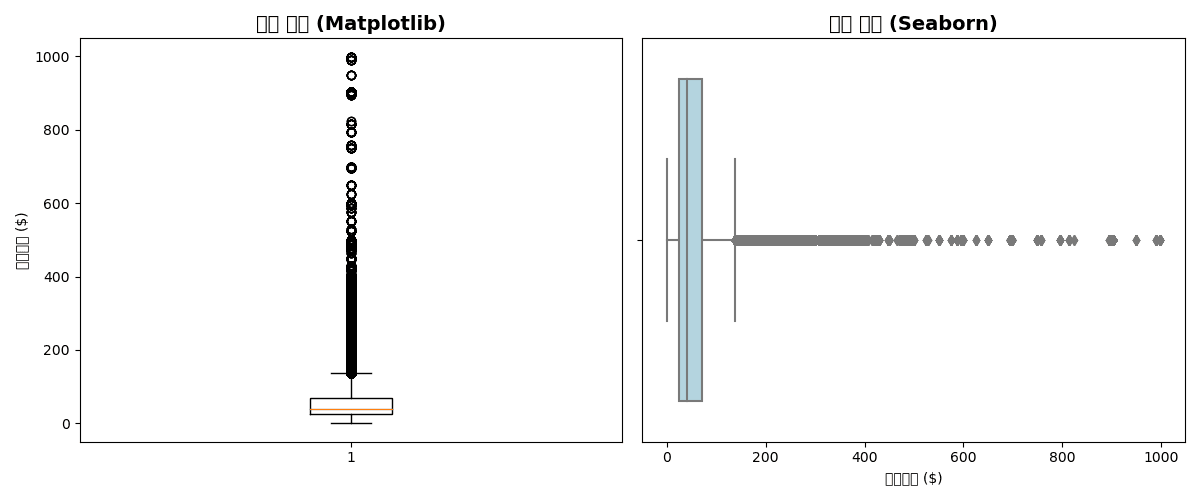
Graph

그룹별 박스플롯


plt.figure(figsize=(14, 6))
 
# 부서별 가격 분포
sns.boxplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    showfliers=True  # 이상치 표시
)
 
plt.title('부서별 판매가격 분포', fontsize=14, fontweight='bold')
plt.xlabel('부서')
plt.ylabel('판매가격 ($)')
plt.tight_layout()
plt.show()
 
# 통계 요약
print("📊 부서별 통계:")
print(df.groupby('department')['sale_price'].describe().round(2))

실행 결과

Error: Could not interpret input 'department'

그룹화된 박스플롯


plt.figure(figsize=(14, 6))
 
# 부서 × 성별
sns.boxplot(
    data=df,
    x='department',
    y='sale_price',
    hue='gender',
    palette=['lightcoral', 'lightblue']
)
 
plt.title('부서/성별 판매가격 분포', fontsize=14, fontweight='bold')
plt.xlabel('부서')
plt.ylabel('판매가격 ($)')
plt.legend(title='성별')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret input 'department'

3. 바이올린 플롯

이론

바이올린 플롯은 박스플롯 + KDE(커널 밀도 추정)의 결합입니다. 분포의 형태를 더 자세히 볼 수 있습니다.

기본 바이올린 플롯


plt.figure(figsize=(14, 6))
 
sns.violinplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    inner='box'  # 내부에 박스플롯
)
 
plt.title('부서별 가격 분포 (바이올린 플롯)', fontsize=14, fontweight='bold')
plt.xlabel('부서')
plt.ylabel('판매가격 ($)')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret input 'department'

inner 옵션


fig, axes = plt.subplots(1, 4, figsize=(16, 4))
inner_options = ['box', 'quartile', 'point', 'stick']
 
for ax, inner in zip(axes, inner_options):
    sns.violinplot(
        data=df,
        x='gender',
        y='sale_price',
        inner=inner,
        ax=ax,
        palette='pastel'
    )
    ax.set_title(f'inner="{inner}"', fontsize=12)
 
plt.suptitle('바이올린 플롯 inner 옵션 비교', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()

실행 결과

[Graph Saved: generated_plot_775a688b4b_0.png]

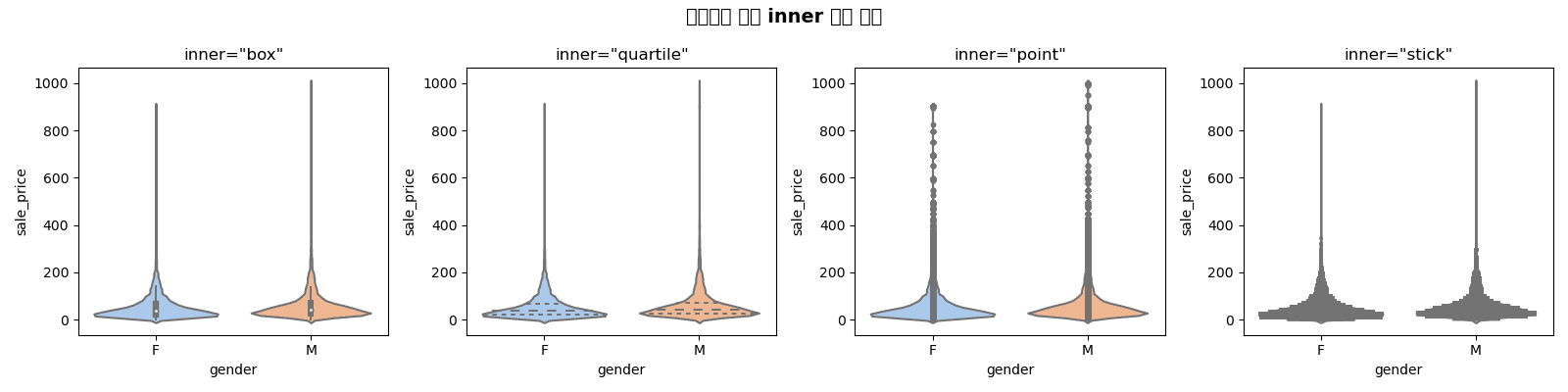
Graph

스플릿 바이올린


plt.figure(figsize=(14, 6))
 
sns.violinplot(
    data=df,
    x='department',
    y='sale_price',
    hue='gender',
    split=True,  # 반쪽씩 표시
    palette=['lightcoral', 'lightblue'],
    inner='quartile'
)
 
plt.title('부서/성별 가격 분포 (스플릿 바이올린)', fontsize=14, fontweight='bold')
plt.xlabel('부서')
plt.ylabel('판매가격 ($)')
plt.legend(title='성별')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret input 'department'

4. KDE 플롯 (커널 밀도 추정)

이론

KDE는 히스토그램을 부드럽게 만든 연속적인 확률 밀도 함수입니다. 분포 형태를 비교할 때 유용합니다.

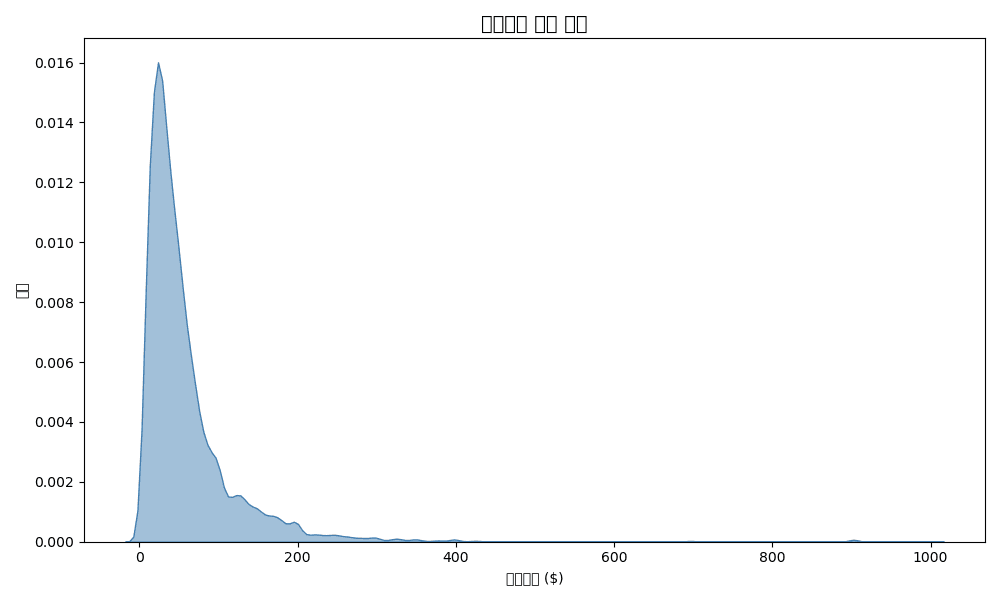
기본 KDE


plt.figure(figsize=(10, 6))
 
# 단일 KDE
sns.kdeplot(df['sale_price'], fill=True, color='steelblue', alpha=0.5)
 
plt.title('판매가격 밀도 분포', fontsize=14, fontweight='bold')
plt.xlabel('판매가격 ($)')
plt.ylabel('밀도')
plt.tight_layout()
plt.show()

실행 결과

[Graph Saved: generated_plot_be63fa9bdc_0.png]

Graph

그룹별 KDE 비교


plt.figure(figsize=(12, 6))
 
# 부서별 KDE
for dept in df['department'].unique():
    dept_data = df[df['department'] == dept]['sale_price']
    sns.kdeplot(dept_data, label=dept, fill=True, alpha=0.3)
 
plt.title('부서별 가격 분포 비교', fontsize=14, fontweight='bold')
plt.xlabel('판매가격 ($)')
plt.ylabel('밀도')
plt.legend(title='부서')
plt.tight_layout()
plt.show()

실행 결과

Error: 'department'

2D KDE (조인트 분포)


plt.figure(figsize=(10, 8))
 
sns.kdeplot(
    data=df,
    x='retail_price',
    y='sale_price',
    cmap='Blues',
    fill=True,
    levels=10,
    thresh=0.05
)
 
plt.title('정가 vs 판매가 조인트 분포', fontsize=14, fontweight='bold')
plt.xlabel('정가 ($)')
plt.ylabel('판매가 ($)')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret value `retail_price` for parameter `x`

5. 종합 분포 플롯

Seaborn JointPlot


# 산점도 + 히스토그램
g = sns.jointplot(
    data=df,
    x='retail_price',
    y='sale_price',
    kind='scatter',
    height=8,
    alpha=0.5
)
g.fig.suptitle('정가 vs 판매가 관계', fontsize=14, fontweight='bold', y=1.02)
plt.show()

실행 결과

Error: Could not interpret value `retail_price` for parameter `x`

PairPlot (다변량 분포)


# 수치형 변수들의 관계
numeric_cols = ['retail_price', 'cost', 'sale_price', 'num_of_item']
sns.pairplot(
    df[numeric_cols].sample(1000),  # 샘플링
    diag_kind='kde',
    plot_kws={'alpha': 0.5}
)
plt.suptitle('수치형 변수 관계', fontsize=14, fontweight='bold', y=1.02)
plt.show()

실행 결과

Error: "['retail_price', 'cost'] not in index"

퀴즈 1: 분포 비교

문제

부서별 판매가격 분포를 다음 3가지 방법으로 비교하세요:

히스토그램 (겹치기, 밀도 정규화)
박스플롯
바이올린 플롯

정답 보기


fig, axes = plt.subplots(1, 3, figsize=(18, 5))
 
# 1. 히스토그램
sns.histplot(
    data=df,
    x='sale_price',
    hue='department',
    stat='density',
    common_norm=False,
    alpha=0.5,
    ax=axes[0]
)
axes[0].set_title('히스토그램', fontsize=12, fontweight='bold')
axes[0].set_xlabel('판매가격 ($)')
 
# 2. 박스플롯
sns.boxplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    ax=axes[1]
)
axes[1].set_title('박스플롯', fontsize=12, fontweight='bold')
axes[1].tick_params(axis='x', rotation=45)
 
# 3. 바이올린 플롯
sns.violinplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    inner='quartile',
    ax=axes[2]
)
axes[2].set_title('바이올린 플롯', fontsize=12, fontweight='bold')
axes[2].tick_params(axis='x', rotation=45)
 
plt.suptitle('부서별 판매가격 분포 비교', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret value `department` for parameter `hue`

퀴즈 2: 이상치 분석

문제

카테고리별 판매가격의 이상치를 분석하세요:

상위 10개 카테고리의 박스플롯 생성
각 카테고리의 이상치 개수 계산
이상치가 가장 많은 카테고리 3개 출력

정답 보기


# 상위 10개 카테고리
top_10_cat = df.groupby('category')['sale_price'].sum().nlargest(10).index
df_top10 = df[df['category'].isin(top_10_cat)]
 
# 박스플롯
plt.figure(figsize=(14, 6))
sns.boxplot(
    data=df_top10,
    x='category',
    y='sale_price',
    palette='Set3',
    order=top_10_cat
)
plt.title('상위 10개 카테고리 가격 분포', fontsize=14, fontweight='bold')
plt.xticks(rotation=45, ha='right')
plt.tight_layout()
plt.show()
 
# 이상치 개수 계산 (IQR 방법)
def count_outliers(group):
    Q1 = group.quantile(0.25)
    Q3 = group.quantile(0.75)
    IQR = Q3 - Q1
    lower = Q1 - 1.5 * IQR
    upper = Q3 + 1.5 * IQR
    return ((group < lower) | (group > upper)).sum()
 
outlier_counts = df_top10.groupby('category')['sale_price'].apply(count_outliers)
outlier_counts = outlier_counts.sort_values(ascending=False)
 
print("📊 카테고리별 이상치 개수:")
print(outlier_counts)
 
print(f"\n🔴 이상치가 가장 많은 카테고리 Top 3:")
for cat, count in outlier_counts.head(3).items():
    print(f"  - {cat}: {count}개")

실행 결과

Error: 'category'

정리

분포 시각화 선택 가이드

목적	추천 차트
단일 변수 분포	히스토그램, KDE
그룹 비교	박스플롯, 바이올린
이상치 탐지	박스플롯
분포 형태 상세	바이올린 + KDE
두 변수 관계	조인트플롯, 2D KDE
다변량 관계	페어플롯

Seaborn 분포 함수 요약

함수	용도	예시
`histplot()`	히스토그램	`sns.histplot(df, x='col')`
`kdeplot()`	KDE	`sns.kdeplot(df['col'])`
`boxplot()`	박스플롯	`sns.boxplot(data=df, x='cat', y='val')`
`violinplot()`	바이올린	`sns.violinplot(data=df, x='cat', y='val')`
`jointplot()`	조인트	`sns.jointplot(data=df, x='x', y='y')`
`pairplot()`	페어	`sns.pairplot(df)`

다음 단계

분포 시각화를 마스터했습니다! 이제 통계 분석 섹션에서 데이터 기반 의사결정을 위한 통계 기법을 배워보세요.