Distribution Visualization

BeginnerIntermediate

Learning Objectives

After completing this recipe, you will be able to:

Understand data distribution with histograms
Detect outliers with box plots
Compare distributions with violin plots
Estimate density with KDE plots

0. Setup

Load CSV files for data practice.


import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
 
# Load Data
# Load Data
orders = pd.read_csv('src_orders.csv', parse_dates=['created_at'])
items = pd.read_csv('src_order_items.csv')
users = pd.read_csv('src_users.csv')
df = orders.merge(items, on='order_id').merge(users, on='user_id')

1. Histogram

Theory

A histogram divides continuous data into intervals (bins) and represents the frequency as bars. It’s useful for understanding the shape of the distribution (normal, skewed, bimodal, etc.).

Basic Histogram


import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
 
# Basic histogram
plt.figure(figsize=(12, 5))
 
plt.subplot(1, 2, 1)
plt.hist(df['sale_price'], bins=30, color='steelblue', edgecolor='white', alpha=0.7)
plt.title('Sale Price Distribution (Matplotlib)', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
plt.ylabel('Frequency')
 
plt.subplot(1, 2, 2)
sns.histplot(df['sale_price'], bins=30, kde=True, color='coral')
plt.title('Sale Price Distribution (Seaborn + KDE)', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
 
plt.tight_layout()
plt.show()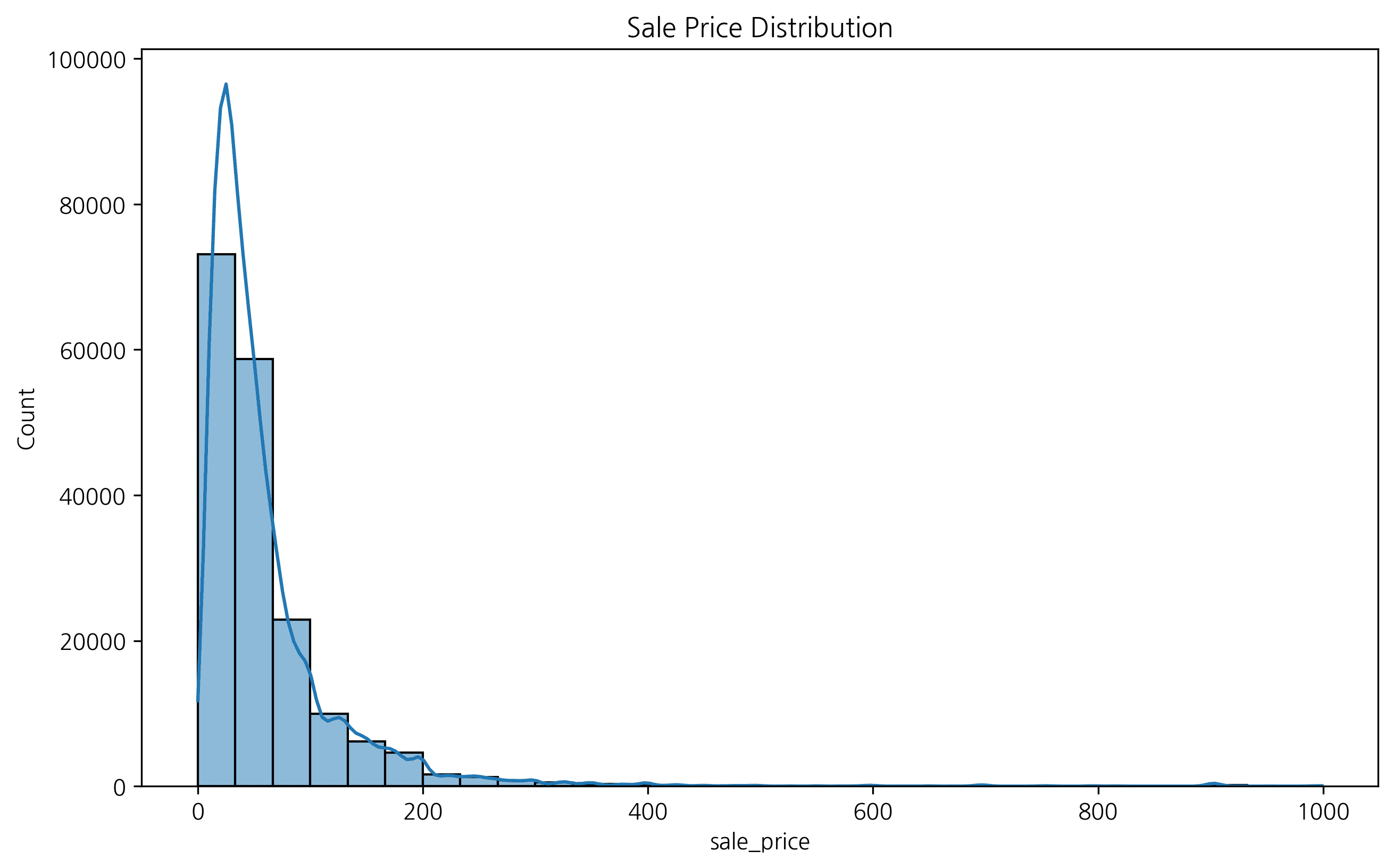

Histogram

2. Setting the Number of Bins

You can adjust the number of histogram bars using the bins parameter. Data interpretation can vary depending on the bin settings.


fig, axes = plt.subplots(1, 3, figsize=(15, 5))
 
sns.histplot(df['sale_price'], bins=10, ax=axes[0], color='skyblue')
axes[0].set_title('Bins = 10')
 
sns.histplot(df['sale_price'], bins=30, ax=axes[1], color='orange')
axes[1].set_title('Bins = 30')
 
sns.histplot(df['sale_price'], bins=50, ax=axes[2], color='green')
axes[2].set_title('Bins = 50')
 
plt.tight_layout()
plt.show()

Histogram Bins Comparison

ℹ️

If there are too few bins, the data characteristics get blurred; if there are too many, noise becomes severe. Proper bin settings are important.

3. Grouped Histogram

You can compare how data distribution differs according to categorical variables. For example, let’s check the sale price distribution by gender.


plt.figure(figsize=(10, 6))
sns.histplot(data=df, x='sale_price', hue='gender', kde=True, element='step')
plt.title('Sale Price Distribution by Gender')
plt.xlabel('Sale Price')
plt.ylabel('Count')
plt.legend(title='Gender')
plt.show()

Grouped Histogram

4. Box Plot

Great for understanding data distribution and outliers at a glance.


plt.figure(figsize=(12, 6))
sns.boxplot(x='category', y='sale_price', data=df)
plt.xticks(rotation=45)
plt.title('Price Distribution by Category')
plt.show()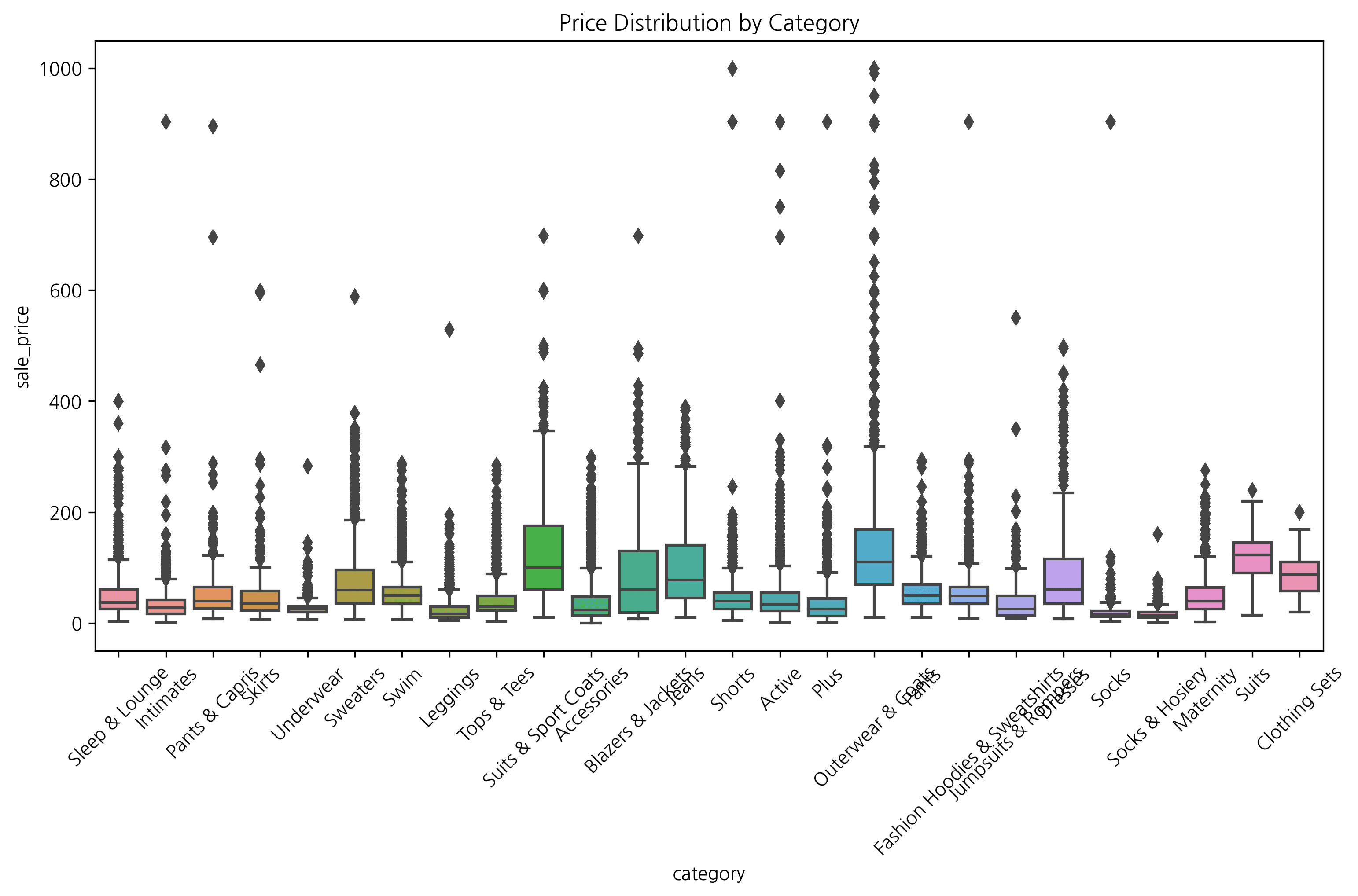

Box Plot

2. Box Plot

Theory

A box plot visualizes the five-number summary (minimum, Q1, median, Q3, maximum) and outliers.

Box Plot Components:

Box: Q1 ~ Q3 (IQR)
Center line: Median
Whiskers: Q1 - 1.5×IQR ~ Q3 + 1.5×IQR
Points: Outliers

Basic Box Plot


plt.figure(figsize=(12, 5))
 
# Matplotlib
plt.subplot(1, 2, 1)
plt.boxplot(df['sale_price'].dropna())
plt.title('Price Distribution (Matplotlib)', fontsize=14, fontweight='bold')
plt.ylabel('Sale Price ($)')
 
# Seaborn (horizontal)
plt.subplot(1, 2, 2)
sns.boxplot(x=df['sale_price'], color='lightblue')
plt.title('Price Distribution (Seaborn)', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
 
plt.tight_layout()
plt.show()

실행 결과

[Graph Saved: generated_plot_1d8420747f_0.png]

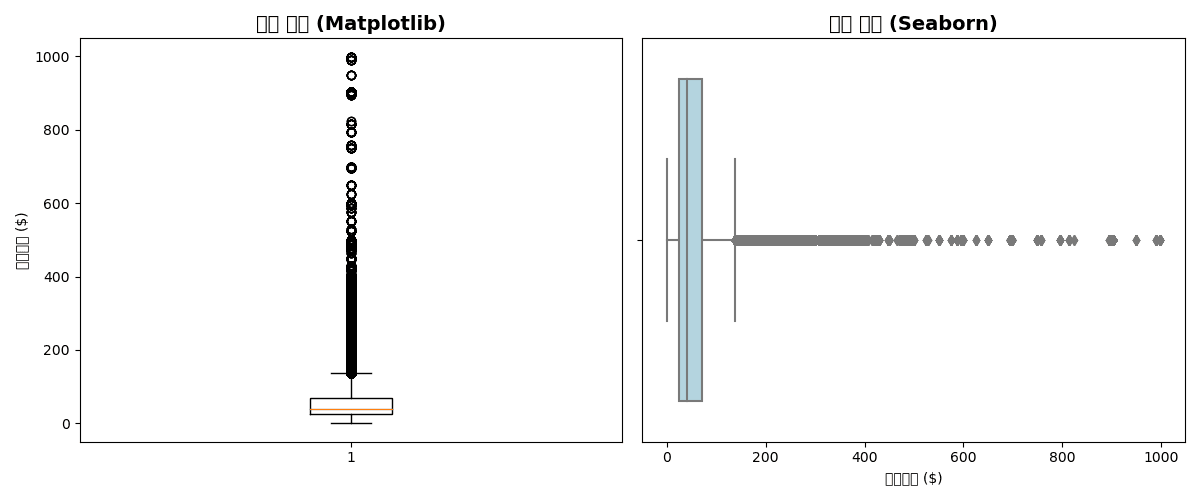
Graph

Box Plot by Group


plt.figure(figsize=(14, 6))
 
# Price distribution by department
sns.boxplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    showfliers=True  # Show outliers
)
 
plt.title('Sale Price Distribution by Department', fontsize=14, fontweight='bold')
plt.xlabel('Department')
plt.ylabel('Sale Price ($)')
plt.tight_layout()
plt.show()
 
# Statistical summary
print("📊 Statistics by Department:")
print(df.groupby('department')['sale_price'].describe().round(2))

실행 결과

Error: Could not interpret input 'department'

Grouped Box Plot


plt.figure(figsize=(14, 6))
 
# Department × Gender
sns.boxplot(
    data=df,
    x='department',
    y='sale_price',
    hue='gender',
    palette=['lightcoral', 'lightblue']
)
 
plt.title('Sale Price Distribution by Department/Gender', fontsize=14, fontweight='bold')
plt.xlabel('Department')
plt.ylabel('Sale Price ($)')
plt.legend(title='Gender')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret input 'department'

3. Violin Plot

Theory

A violin plot is a combination of box plot + KDE (kernel density estimation). It allows you to see the shape of the distribution in more detail.

Basic Violin Plot


plt.figure(figsize=(14, 6))
 
sns.violinplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    inner='box'  # Box plot inside
)
 
plt.title('Price Distribution by Department (Violin Plot)', fontsize=14, fontweight='bold')
plt.xlabel('Department')
plt.ylabel('Sale Price ($)')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret input 'department'

Inner Options


fig, axes = plt.subplots(1, 4, figsize=(16, 4))
inner_options = ['box', 'quartile', 'point', 'stick']
 
for ax, inner in zip(axes, inner_options):
    sns.violinplot(
        data=df,
        x='gender',
        y='sale_price',
        inner=inner,
        ax=ax,
        palette='pastel'
    )
    ax.set_title(f'inner="{inner}"', fontsize=12)
 
plt.suptitle('Violin Plot Inner Options Comparison', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()

실행 결과

[Graph Saved: generated_plot_775a688b4b_0.png]

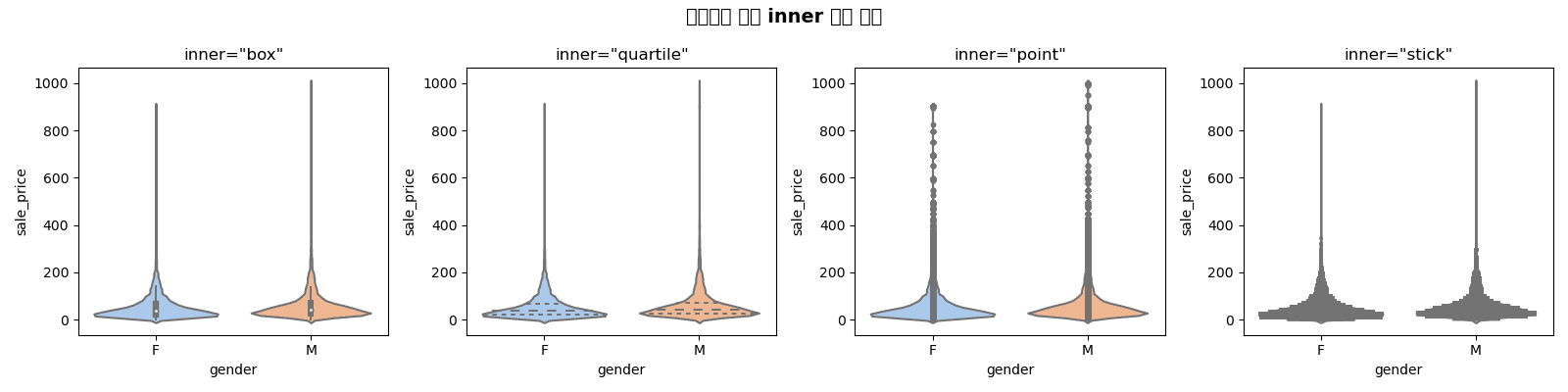
Graph

Split Violin


plt.figure(figsize=(14, 6))
 
sns.violinplot(
    data=df,
    x='department',
    y='sale_price',
    hue='gender',
    split=True,  # Show half on each side
    palette=['lightcoral', 'lightblue'],
    inner='quartile'
)
 
plt.title('Price Distribution by Department/Gender (Split Violin)', fontsize=14, fontweight='bold')
plt.xlabel('Department')
plt.ylabel('Sale Price ($)')
plt.legend(title='Gender')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret input 'department'

4. KDE Plot (Kernel Density Estimation)

Theory

KDE is a continuous probability density function that smooths a histogram. It’s useful for comparing distribution shapes.

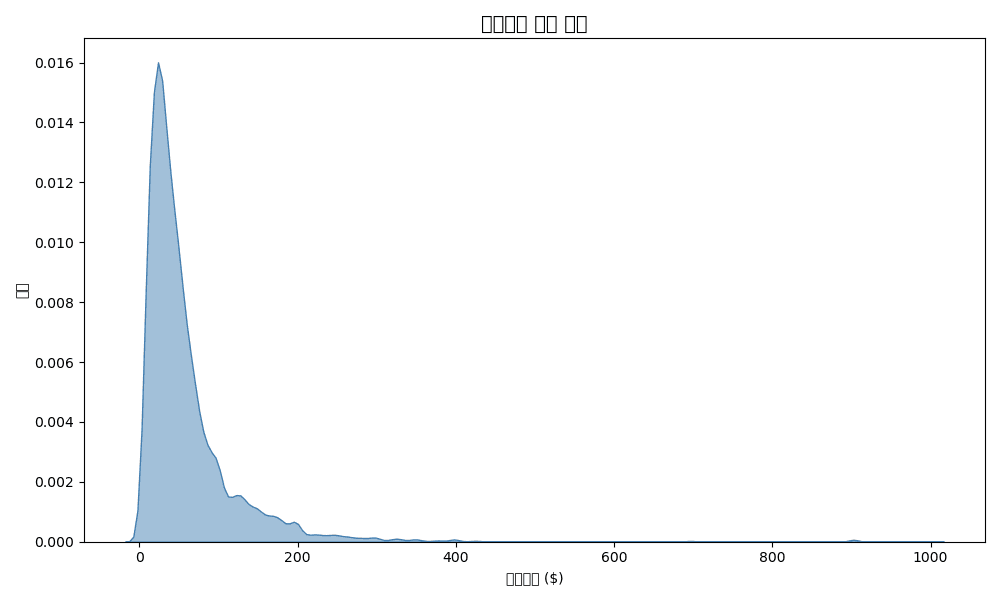
Basic KDE


plt.figure(figsize=(10, 6))
 
# Single KDE
sns.kdeplot(df['sale_price'], fill=True, color='steelblue', alpha=0.5)
 
plt.title('Sale Price Density Distribution', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
plt.ylabel('Density')
plt.tight_layout()
plt.show()

실행 결과

[Graph Saved: generated_plot_be63fa9bdc_0.png]

Graph

KDE Comparison by Group


plt.figure(figsize=(12, 6))
 
# KDE by department
for dept in df['department'].unique():
    dept_data = df[df['department'] == dept]['sale_price']
    sns.kdeplot(dept_data, label=dept, fill=True, alpha=0.3)
 
plt.title('Price Distribution Comparison by Department', fontsize=14, fontweight='bold')
plt.xlabel('Sale Price ($)')
plt.ylabel('Density')
plt.legend(title='Department')
plt.tight_layout()
plt.show()

실행 결과

Error: 'department'

2D KDE (Joint Distribution)


plt.figure(figsize=(10, 8))
 
sns.kdeplot(
    data=df,
    x='retail_price',
    y='sale_price',
    cmap='Blues',
    fill=True,
    levels=10,
    thresh=0.05
)
 
plt.title('Retail Price vs Sale Price Joint Distribution', fontsize=14, fontweight='bold')
plt.xlabel('Retail Price ($)')
plt.ylabel('Sale Price ($)')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret value `retail_price` for parameter `x`

5. Combined Distribution Plots

Seaborn JointPlot


# Scatter plot + Histogram
g = sns.jointplot(
    data=df,
    x='retail_price',
    y='sale_price',
    kind='scatter',
    height=8,
    alpha=0.5
)
g.fig.suptitle('Retail Price vs Sale Price Relationship', fontsize=14, fontweight='bold', y=1.02)
plt.show()

실행 결과

Error: Could not interpret value `retail_price` for parameter `x`

PairPlot (Multivariate Distribution)


# Relationships between numeric variables
numeric_cols = ['retail_price', 'cost', 'sale_price', 'num_of_item']
sns.pairplot(
    df[numeric_cols].sample(1000),  # Sampling
    diag_kind='kde',
    plot_kws={'alpha': 0.5}
)
plt.suptitle('Numeric Variable Relationships', fontsize=14, fontweight='bold', y=1.02)
plt.show()

실행 결과

Error: "['retail_price', 'cost'] not in index"

Quiz 1: Distribution Comparison

Problem

Compare the sale price distribution by department using these 3 methods:

Histogram (overlapping, density normalized)
Box plot
Violin plot

View Answer


fig, axes = plt.subplots(1, 3, figsize=(18, 5))
 
# 1. Histogram
sns.histplot(
    data=df,
    x='sale_price',
    hue='department',
    stat='density',
    common_norm=False,
    alpha=0.5,
    ax=axes[0]
)
axes[0].set_title('Histogram', fontsize=12, fontweight='bold')
axes[0].set_xlabel('Sale Price ($)')
 
# 2. Box plot
sns.boxplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    ax=axes[1]
)
axes[1].set_title('Box Plot', fontsize=12, fontweight='bold')
axes[1].tick_params(axis='x', rotation=45)
 
# 3. Violin plot
sns.violinplot(
    data=df,
    x='department',
    y='sale_price',
    palette='Set2',
    inner='quartile',
    ax=axes[2]
)
axes[2].set_title('Violin Plot', fontsize=12, fontweight='bold')
axes[2].tick_params(axis='x', rotation=45)
 
plt.suptitle('Sale Price Distribution Comparison by Department', fontsize=14, fontweight='bold')
plt.tight_layout()
plt.show()

실행 결과

Error: Could not interpret value `department` for parameter `hue`

Quiz 2: Outlier Analysis

Problem

Analyze sale price outliers by category:

Create box plots for the top 10 categories
Calculate the number of outliers for each category
Print the 3 categories with the most outliers

View Answer


# Top 10 categories
top_10_cat = df.groupby('category')['sale_price'].sum().nlargest(10).index
df_top10 = df[df['category'].isin(top_10_cat)]
 
# Box plot
plt.figure(figsize=(14, 6))
sns.boxplot(
    data=df_top10,
    x='category',
    y='sale_price',
    palette='Set3',
    order=top_10_cat
)
plt.title('Price Distribution for Top 10 Categories', fontsize=14, fontweight='bold')
plt.xticks(rotation=45, ha='right')
plt.tight_layout()
plt.show()
 
# Calculate outlier count (IQR method)
def count_outliers(group):
    Q1 = group.quantile(0.25)
    Q3 = group.quantile(0.75)
    IQR = Q3 - Q1
    lower = Q1 - 1.5 * IQR
    upper = Q3 + 1.5 * IQR
    return ((group < lower) | (group > upper)).sum()
 
outlier_counts = df_top10.groupby('category')['sale_price'].apply(count_outliers)
outlier_counts = outlier_counts.sort_values(ascending=False)
 
print("📊 Outlier Count by Category:")
print(outlier_counts)
 
print(f"\n🔴 Top 3 Categories with Most Outliers:")
for cat, count in outlier_counts.head(3).items():
    print(f"  - {cat}: {count}")

실행 결과

Error: 'category'

Summary

Distribution Visualization Selection Guide

Purpose	Recommended Chart
Single variable distribution	Histogram, KDE
Group comparison	Box plot, Violin
Outlier detection	Box plot
Detailed distribution shape	Violin + KDE
Two variable relationship	Joint plot, 2D KDE
Multivariate relationship	Pair plot

Seaborn Distribution Function Summary

Function	Purpose	Example
`histplot()`	Histogram	`sns.histplot(df, x='col')`
`kdeplot()`	KDE	`sns.kdeplot(df['col'])`
`boxplot()`	Box plot	`sns.boxplot(data=df, x='cat', y='val')`
`violinplot()`	Violin	`sns.violinplot(data=df, x='cat', y='val')`
`jointplot()`	Joint	`sns.jointplot(data=df, x='x', y='y')`
`pairplot()`	Pair	`sns.pairplot(df)`

Next Steps

You’ve mastered distribution visualization! Now learn statistical techniques for data-driven decision making in the Statistical Analysis section.